最优化问题的分类是多样的。按照是否存在约束条件,最优化问题可以分为无约束优化问题和约束优化问题两大类型。
无约束优化在生活中是一种比较常见的优化问题,也是我们接触的比较早的问题。一般的来说,无约束优化问题可以被看作求一个函数的极值问题,即
其中,被称为决策变量,
被称为目标函数。使得
达到极小的
被称为上述优化问题的解,记为
,而
则是该优化问题的最优值。该问题有一种等价的写法:
而如果以上问题受到了某些条件的限制,那么该问题便成了一个约束优化问题,即
这里,是"subject to"的缩写,意为“满足于”,一般的,在
之后的表达式被称为该约束优化问题的约束条件。
被称为约束函数,其中
是等式约束,
是不等式约束,
和
在一起被称为约束的指标集合。
以上的两种优化问题是最基本的两种问题,一般来说所有优化问题均可以被变换为这两种形式。特别的,如果是求极大值问题,我们可以取目标函数的相反数,使其变为求极小值问题,即
。
本节开始,我们首先讨论无约束优化问题。
一般的来说,对于无约束优化问题,它的最优解可以分为全局最优解与局部最优解。
Def 1.1: 在以下无约束优化问题中:
(1). 若对于任意的,
,则称
为该问题的全局最优解;如果
,则称
为该问题的严格全局最优解。
(2). 对于,若存在
,使得对于任意
,当
时,有
,则称
为该问题的局部最优解;同理,如果
,则称
为该问题的严格局部最优解。
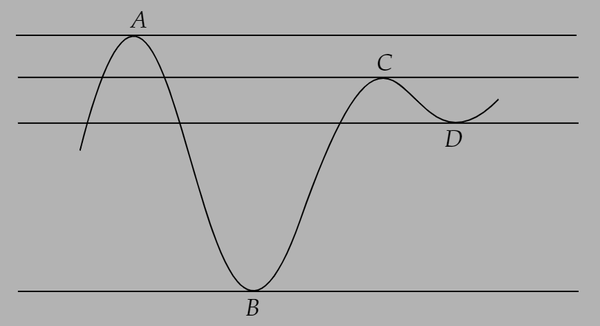
如以上图中所示,和
两点为曲线的严格全局最优解,而
和
两点则为局部最优解。
在实际问题中,全局最优解往往不存在或者难以达到。因此往往局部最优解是我们所希望的,本专题中介绍的所有算法,如不特殊说明,则都是求局部最优解的算法。
首先一个问题是我们如何保证最优解的存在性呢?考虑一般的无约束优化问题,如果目标函数是连续的,且定义域是紧的,那么我们很容易得出最优解的存在性。但是如果以上两个条件中有其一不成立,都会导致目标函数在定义域上的不可微性质,这时候我们无法直接判断其解的存在性。
我们需要一个工具把以上的集中情况全部集中起来讨论。考虑到在数学分析中,我们学过Weierstrass定理,其保证了紧集上的连续函数的最值点的存在性。下面我们将这一定理进行推广。
我们需要一些工具来辅助说明。
Def 1.2: 令为广义实数空间,则映射
为广义实值函数。
Def 1.3: 给定广义实值函数和非空集合
。如果存在
使得
,且对于任意的
,都有
,则称函数关于集合
是适当的。
Def 1.4: 对于一个广义实值函数,对于任意的
,有
则称为下半连续函数。
Def 1.5: 对于一个广义实值函数,
是的一个
-下水平集。而
称为的上镜图。
实际上,下水平集就是的定义域中所有函数值不大于
的点的集合。而上镜图则反映了函数
和
的上方区域。下面是一个函数的上镜图。
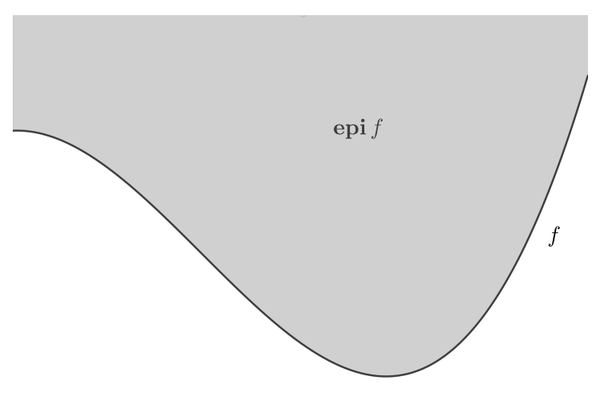
特别的,如果上镜图是闭集,则称对应的
为闭函数。
Lemma 1.6: 对于一个广义实值函数,以下命题等价:
(1).是下半连续的;
(2).的任意
-下水平集都是闭集;
(3).是闭函数。
Proof: 设(1)成立,令且
,根据下半连续性,有
这等价于,即上镜图是闭集。即(3)成立。
再设(3)成立。取下水平集中的元素
,注意到
且
,由
为闭集可知
,即
,从而(2)成立。
最后设(2)成立,假设存在一个序列但
,取
使得
根据下极限的定义,中必定包含无穷个
,假设
中存在子列
使得
且
,这与
-下水平集为闭集矛盾,因此(1)成立。
根据以上一系列的工具,我们可以得到以下的推广版本的Weierstrass定理。
Thm 1.7:(Weierstrass定理) 考虑一个合适的闭的函数,如果函数满足以下三个条件中的任意一个,则问题
的最小值点集
是非空的紧集。
(1).定义域是有界的;
(2).存在一个常数使得下水平集:
非空有界。
(3).对于任意满足范数趋于无穷的点列,即
,有
Proof: 假设(1)成立,则是有界的。由于存在
使得
,令
,则下水平集
非空有界。
假设(3)成立,假设无界,则存在点列
满足
,但根据(3),有
,这与
矛盾,因此
非空有界。
这样,条件(1)和(3)都可以转化为条件(2)。下面证明条件(2)成立即可。
采用反证法,假设,则存在点列
,使得
。因为
的有界性,点列必定存在聚点,记为
。由于
,且上镜图是闭的,这与函数的适当性矛盾,从而
。
由于,且
是下确界,故必定有
,即下确界可以取到,根据引理Lemma 1.6和
的有界性,可知最小值点是紧的。
定理Thm 1.7中的三个条件本质上都是再保证的最小值无法再无穷远处取得,从而我们可以只在一个有界的下水平集中考虑
的最小值,且不要求函数
的连续性。
我们可以举例说明以上定理的适用性。对于函数和
,定义域均为
,前者满足定理Thm 1.7中的条件(3),因此存在最小值,而后者不满足以上三个条件中的任意一个,从而最小值不存在。
上述Weierstrass定理只保证了最优解的存在性,但无法确定是否是唯一的。最优化问题解的唯一性在理论分析和算法比较中扮演着重要角色.比如,假设问题(1.1)的解是唯一存在的,记为,那么不同的算法最终都会收敛到
。此时,我们通过比较不同算法的收敛速度来判断算法好坏是非常合理的。但是如果问题(1.1)存在多个最优值点,不同的算法收敛到的最优值点可能不同,那么这些算法收敛速度的比较就失去了参考价值。
我们考虑函数是强拟凸的情况。
Def 1.8: 给定凸集和函数
,如果对于任意的
和
,有
则称函数是强拟凸的。
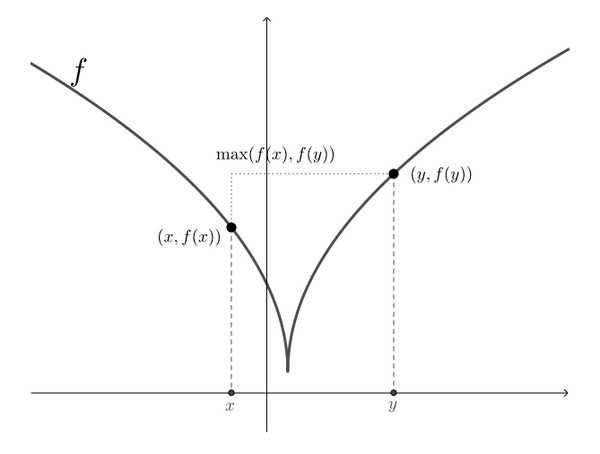
强拟凸函数的几何意义是定义域内任何两点之间线段上的函数值不会大于两个端点处函数值的最大值,一般来说,强拟凸函数不一定是凸函数,但其任意一个下水平集都是凸集,并可以包含一部分性质较好的非凸函数。任意强凸函数均为强拟凸的,但凸函数并不一定是强拟凸的。
下面是一个强拟凸函数的示意图。
Thm 1.9: 对于问题(1.1),设是
的一个非空,紧凸集,如果
是适当,闭且强拟凸的函数,则存在唯一的
满足
Proof: 根据Weierstrass定理,问题(1.1)至少存在一个全局最优解,假设还存在另外一个全局最优解,则
。由强拟凸函数的定义,对于任意的
,
这与的全局最优性矛盾。
如果能将抽象的优化问题化为直观的图像,这是我们所期待的。一般的来说,对于一维问题,这是容易的。三维以上的问题可能无法实现,而对于二维问题,我们需要通过平面图的方式对其进行呈现。
由于二维问题的图像是立体的,我们需要借助等高线对其进行描述。所谓等高线,指的是,函数图像上函数值恒等于一个常数的所有点的集合,根据常数的不同,我们可以得到一簇等高线族。
例如,考虑以下函数:
这个函数叫做Rosenbrock函数,是一个非常著名的检验函数,其极小值点为。
下图给出了这个函数的图像和等高线描述,其中黑点表示函数的极小点,等高线图中的颜色越浅表示函数值越小.该函数等高线的形状犹如一个香蕉,所以我们也称该函数为香蕉函数。
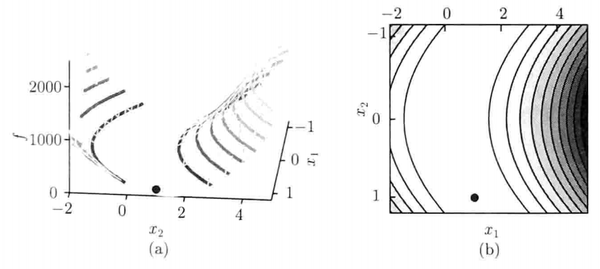
满足的点称为稳定点.由最优性条件可知,函数的极小点一定是稳定点,反之则不一定.那么稳定点有几种类型呢?我们知道极小点和极大点均为稳定点. 以有极大点和有极小点的二维函数
为例,它们的共同之处在于函数在极小值与极大值处的切平面平行于
平面。既非极小点又非极大点的稳定点为鞍点。这几种情形的二维函数的图形与等高线见下图。
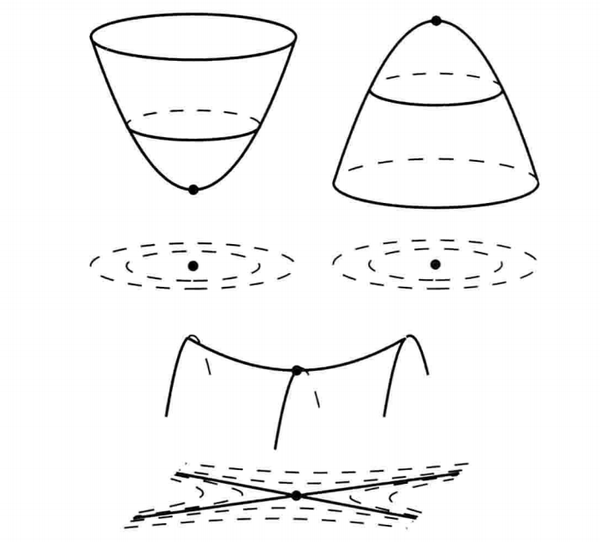
根据图像我们可以看出,求极大值的问题类似于一个登山的过程,我们沿着一条路径到达山顶。同样,求极小值的问题类似于探索山谷,我们顺着一条路径到达谷底。而优化算法,就是在说明在这个过程中如何选取路径是最好的,从而满足不同的需求。这是优化问题的形象表述。
本文使用 Zhihu On VSCode 创作并发布