新闻资讯

服务热线400-123-4567

常见问答

SGD和Adam优化器的区别是什么？_1

作者：佚名发布时间：2024-08-26 05:23:20点击：

看了很多文章是介绍这种具体原理的，也有文章中提到很多paper坚持通过调参使用SGD，Adam被认为是“傻瓜优化器”，但是从SGD的缺点来看，在鞍点或峡谷似的解空间中收敛非常慢，Adam至少不存在这种问题，而且Adam还结合了SGDM与RMSprop，通过一阶矩可以得到惯性保持，通过二阶矩拥有了环境感知的能力，那两者的这种优势和弱势都体现在哪，或SGD、Adam各自都擅长在哪些领域发挥出它们自身的优势

Adam相对SGD优化器强太多了，在对参数的初始化上，超参的设定上都有很大的优势。

怎么快速训练LLM也是LLM快速落地应用中的重要一环，新出的Sophia优化器是近期斯坦福新提出的方案之一。刚好有知友 @Michael在问这个新的Sophia优化器效果怎么样，我也想验证下效果和可借鉴的点，特此记录分享一下。

从下图通过直观感受，能看到Sophia优化器比我们常用的Adam需要更少的步数从 $初始参数\ heta_{0}到最优点\ heta^{*}$ 。论文结论是训练同一个nanoGPT模型，使用优化器Sophia比Adam速度快2倍。

git clone https://github.com/Liuhong99/Sophia.git
conda create -n sophia python==3.8
conda activate sophia
pip install torch==2.0 transformers datasets tiktoken wandb -i https://mirror.baidu.com/pypi/simple

https://huggingface.co/datasets/openwebtext （示例数据）示例数据蛮大的。

stas/openwebtext-10k · Datasets at Hugging Face （示例数据的弟弟）想快速体验的可先用这个小数据

先下载数据，网络稳定网速好的同学可跳过下载部分，直接运行Sophia/data/openwebtext/prepare.py，会自动下载数据和预处理。

下载大数据链接经常中断的可试下博主土办法, low但管用.

#新建download.py

import time
from datasets import load_dataset # huggingface datasets
while True:
	try:
		dataset = load_dataset("openwebtext" )
	except Exception as e:
		time.sleep(2)
		print("链接失败...., 重试")
		continue
	print("good boy. ")
	breaks

下载完了，再运行预处理脚本: Sophia/data/openwebtext/prepare.py

PS: 可能会遇到路径错误bug, 根据情况修改即可

单卡24G刚好够跑这个小的 123.59M参数。由于数据下载的原因，先跑了一个10k的小数数据。

昨天大数据没下载完，想着用10K的小数据跑下验证下效果。但从10k数据暂时观察不到明显的收益，adam和sophia的收敛速度差不多，差距不明显，应该是数据太少没有拉开明显的差距?。训练结果如下图

# 参数啥也没改，数据换成了10k的数据
# train small GPT2 with sophia
torchrun --standalone --nproc_per_node=1 train_sophiag.py \\
config/train_gpt2_small_sophiag.py --batch_size=8 \\
--gradient_accumulation_steps=6

# train small GPT2 with adam
torchrun --standalone --nproc_per_node=1 train_adam.py \\
config/train_gpt2_small_adam.py --batch_size=8 \\
--gradient_accumulation_steps=6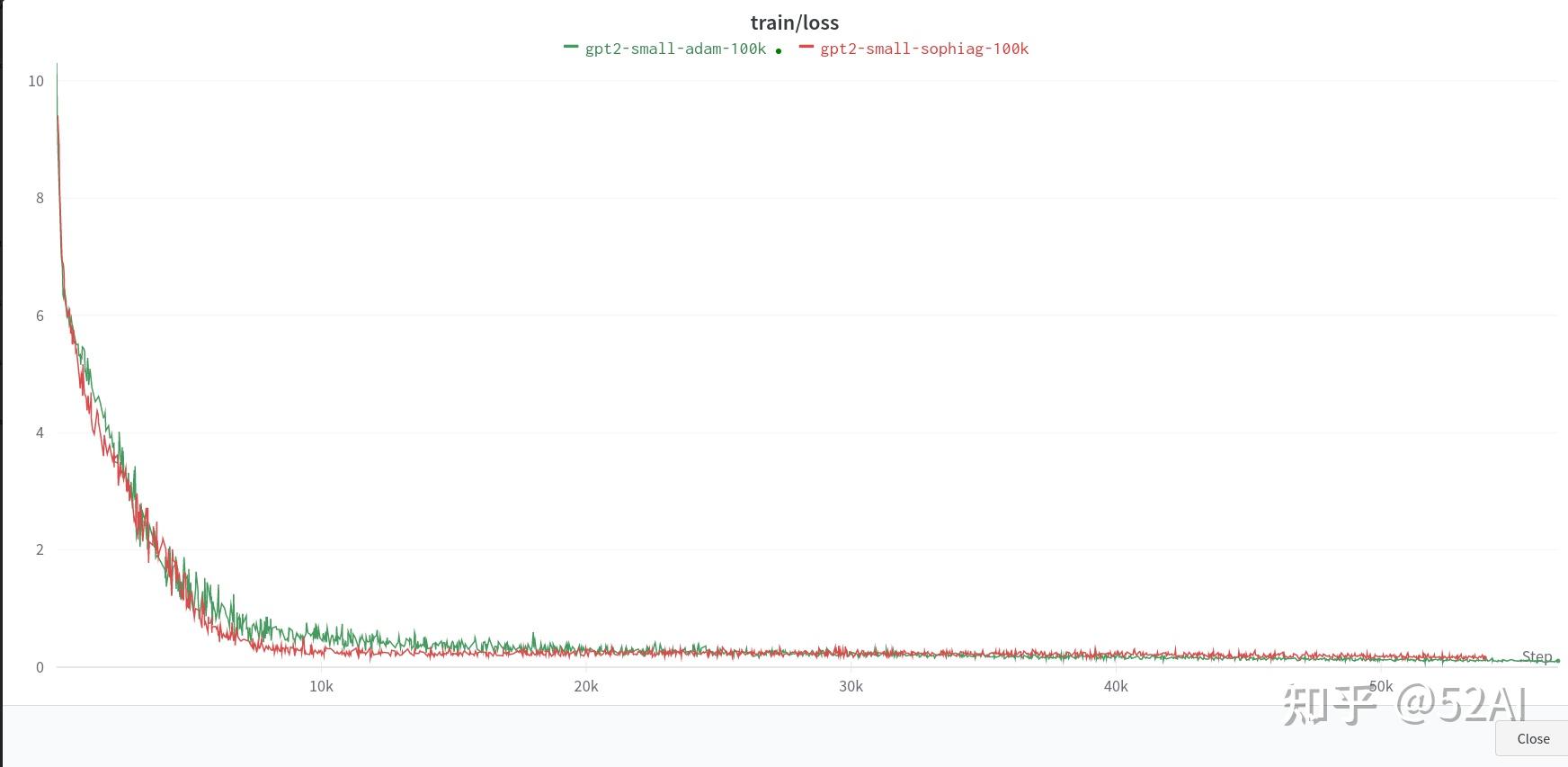

# 参数啥也没改，数据换成了全量的数据
# train small GPT2 with sophia
torchrun --standalone --nproc_per_node=1 train_sophiag.py \\
config/train_gpt2_small_sophiag.py --batch_size=8 \\
--gradient_accumulation_steps=6

# train small GPT2 with adam
torchrun --standalone --nproc_per_node=1 train_adam.py \\
config/train_gpt2_small_adam.py --batch_size=8 \\
--gradient_accumulation_steps=6

全量数据 + 单卡3090 : 无明显收敛速度上的提升。

这里使用作者示例中的全量数据, 和上面训练同一个小参数的模型的结果，默认参数，单卡.

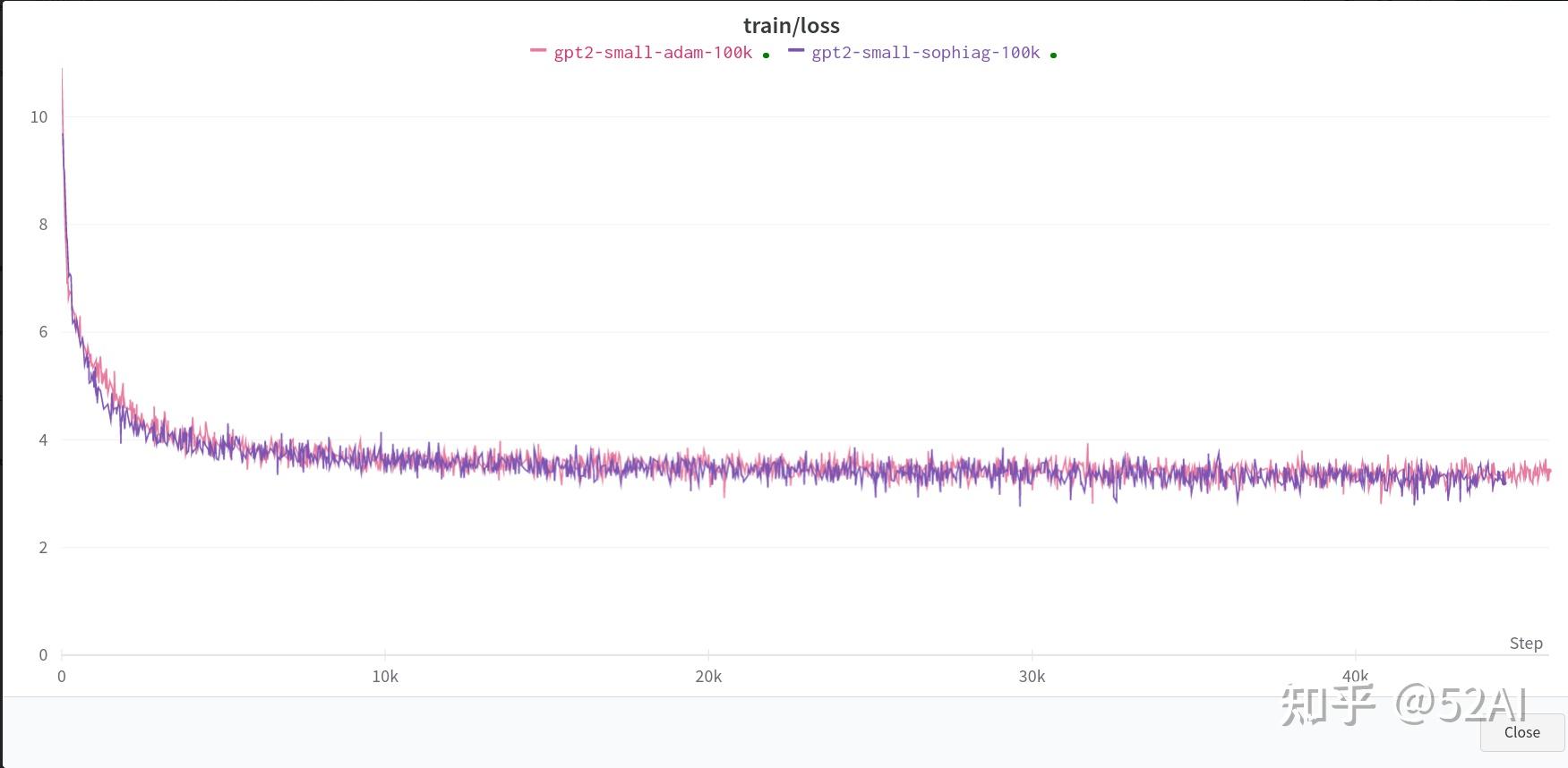
全量数据 + 2x3090测试结果：能看到一点Sophia比Adam模型收敛更快的效果,但并没到2x的效果.

# 参数啥也没改，数据换成了全量的数据，2 x 3090 
# train small GPT2 with sophia
torchrun --standalone --nproc_per_node=2 train_sophiag.py \\
config/train_gpt2_small_sophiag.py --batch_size=8 \\
--gradient_accumulation_steps=6

# train small GPT2 with adam
torchrun --standalone --nproc_per_node=2 train_adam.py \\
config/train_gpt2_small_adam.py --batch_size=8 \\
--gradient_accumulation_steps=6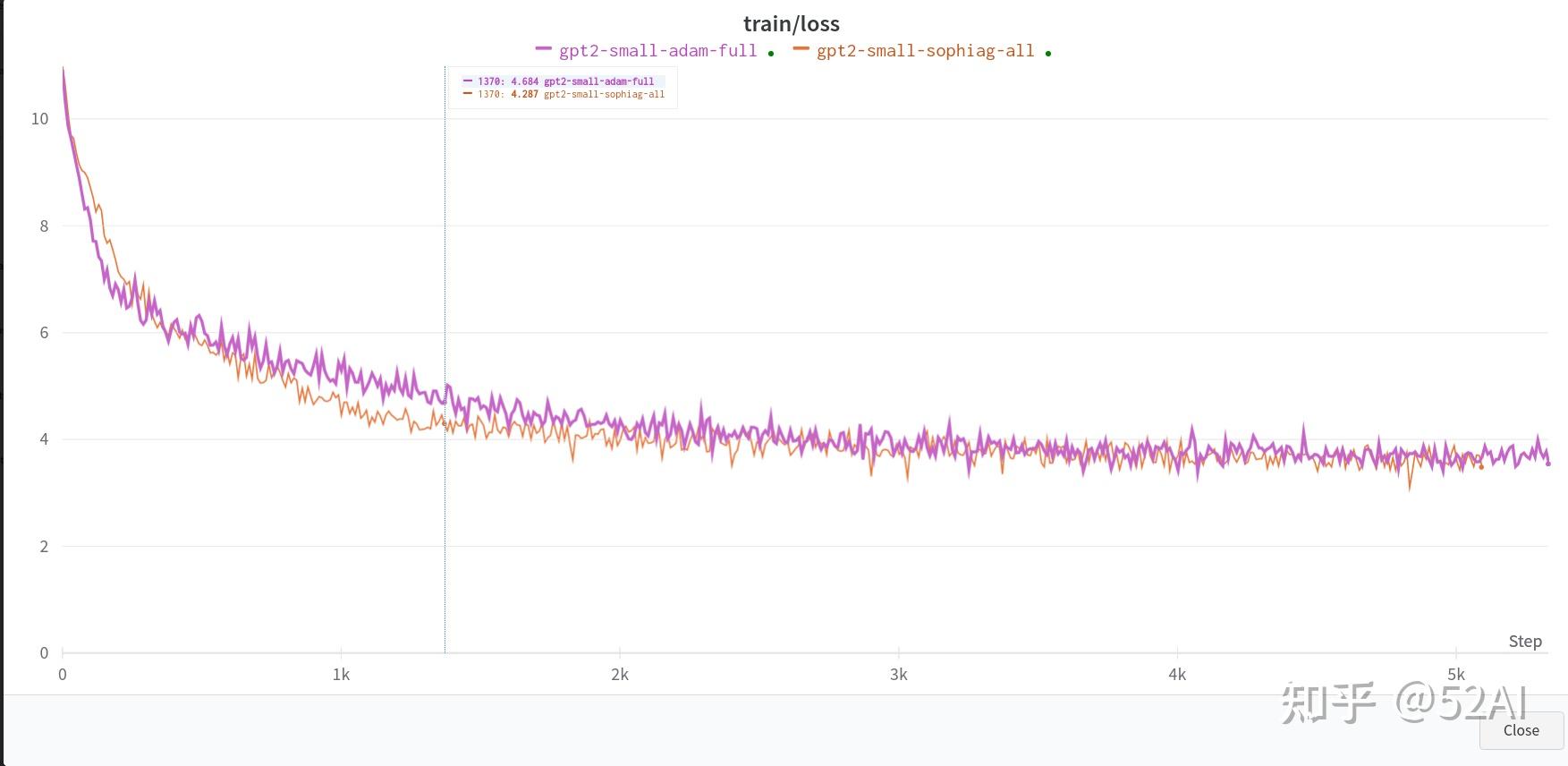

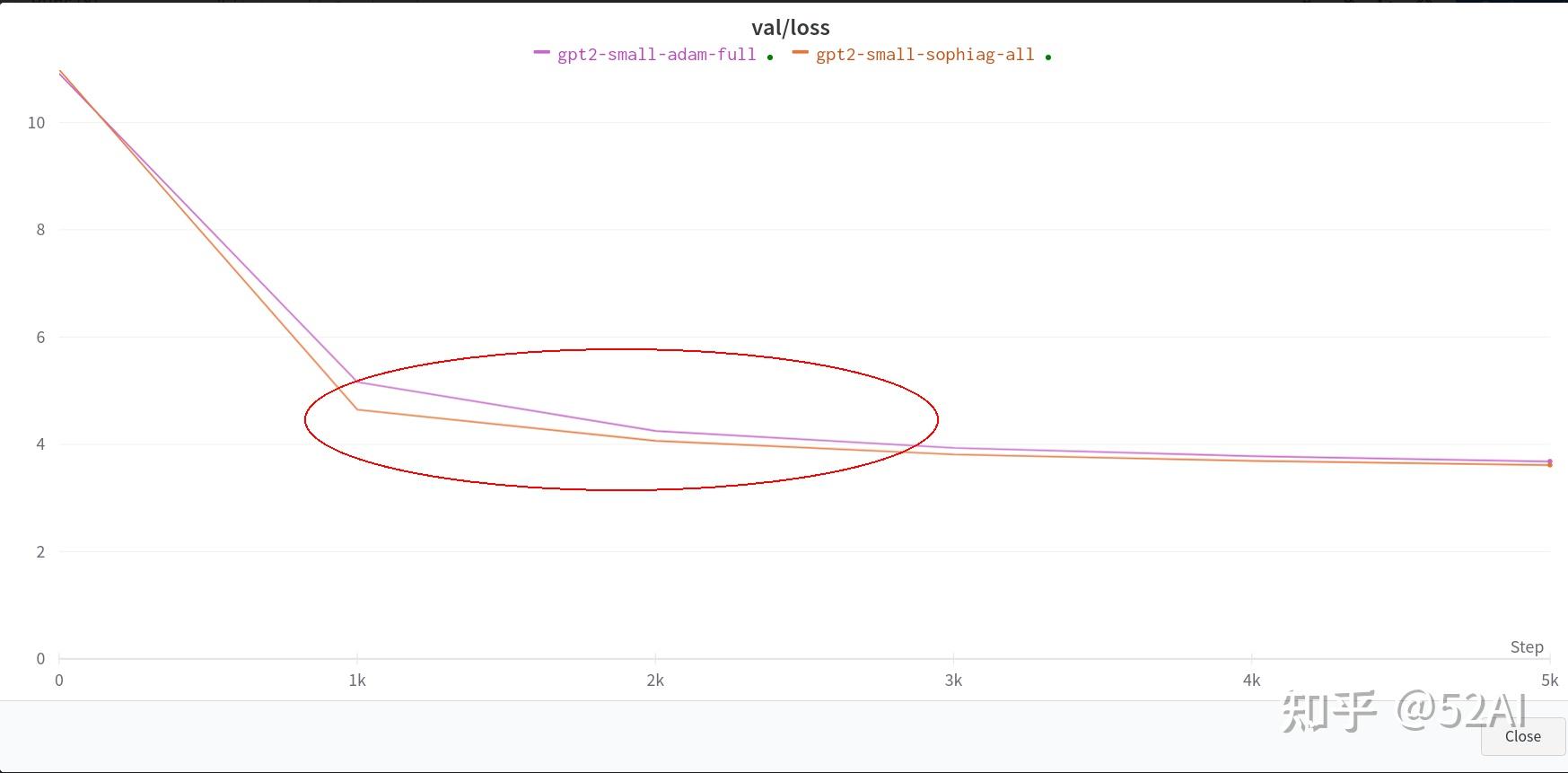
当然示例使用的是10 x 24G跑的，没那么多卡来验证, 可看下作者放出来的小模型对比训练结果，官方示例中Sophia的收敛速度优势体现是比较明显的。

Sophia适用从头训练大模型, 且在batchsize更大的时候训练速度提升效果会更明显，小batchsize参数训练, Adam和Sophia不会有啥明显速度提升效果。因此像做LLM高效微调，可能收益并不会很明显。

参考

code: https://github.com/Liuhong99/Sophia

paper : Sophia: A Scalable Stochastic Second-order Optimizer for Language Model Pre-training

————————————————————————

@52AI | 点赞关注不迷路 · 持续关注更新计算机视觉和自然语言处理的前沿技术

以一个小球在山谷上滚落比喻解释，SGD和 Adam算法的区别。

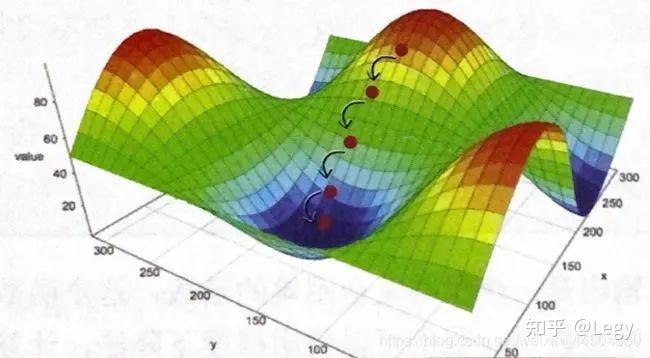
假设我们有一个小球位于山谷的某个位置，我们的目标是让这个小球滚到山谷的最低点。将山谷看作是一个多维空间，小球的位置表示我们在这个空间中的参数，而山谷的形状则表示损失函数的形态，我们的目标是找到参数值，使得损失函数取得最小值，即小球滚到山谷的最低点。

SGD 就是让小球在山谷中沿着当前位置的梯度方向下降的过程。梯度表示损失函数在当前位置的变化率，沿着梯度的反方向更新参数，就相当于让小球朝着最陡峭的下坡方向滚动，逐步接近山谷的最低点。

SGD 算法使用固定的学习率来控制每次更新的步幅。学习率的大小直接影响了小球在山谷中滚动的速度。如果学习率太大，可能会导致小球在山谷中震荡或错过最低点，而如果学习率太小，小球的下降速度会很慢，需要更多的迭代次数才能到达最低点。

Adam

Adam 算法可以看作是在 SGD 的基础上进行了优化，它结合了梯度的一阶矩估计和二阶矩估计来动态调整学习率，使得小球能够更加智能地滚动到山谷的最低点。

具体来说，Adam 算法会根据梯度的一阶矩估计（平均梯度当前的山谷斜率）和二阶矩估计（平方梯度的平均 当前斜率的变化程度）来计算每个参数的自适应学习率。这样做的好处是，它可以在训练的初期使用较大的学习率来快速收敛，而在训练的后期自动降低学习率，避免震荡或错过最低点的问题。

Adam 算法也可以看作是在梯度下降中引入了一种"动量"的概念，使得小球在山谷中更具有惯性，有助于克服一些局部最优解，更可能找到全局最优解。

尽管Adam算法在许多情况下表现良好，但有时候可能会出现其效果不如SGD的情况。这种现象可能由以下几个因素导致：

超参数设置：Adam算法有几个需要手动设置的超参数，如学习率（learning rate）、β1和β2（用于计算梯度的一阶和二阶矩估计的衰减率）以及?（用于数值稳定性的小值）。不恰当的超参数设置可能导致性能下降，例如过大的学习率可能导致震荡，而过小的学习率可能导致收敛缓慢。
数据集和模型的特性：算法的性能通常取决于数据集和模型的特性。对于某些数据集和模型，SGD的简单性和随机性可能表现得更好，而Adam的自适应学习率可能在这些情况下过于复杂，导致不稳定的训练过程。
优化目标的非凸性：在某些情况下，优化目标可能具有非凸性（存在多个局部最优解），在这种情况下，SGD可能会因其随机性而更有可能跳出局部最优解，而Adam由于引入了一些惯性可能会陷入其中。
训练数据集大小：Adam算法使用梯度的二阶矩估计，可能需要更多的内存来存储历史梯度信息。当训练数据集非常大时，这可能会导致内存限制或计算资源不足的问题。
过拟合：Adam算法的自适应学习率可能在训练初期过快地收敛，导致在某些情况下更容易过拟合训练数据。

有时候，简单的SGD或SGD的变种可能会表现出意想不到的优势，特别是在小数据集或简单模型的情况下。

通俗的理解一阶矩估计和二阶矩估计

一阶矩估计：想象一下你在山谷中，想要找到山谷最低点。一阶矩估计就是告诉你当前位置的斜率信息。在优化算法中，斜率对应损失函数的梯度，它告诉我们当前位置朝哪个方向是最陡峭的下坡，从而让我们能够更新模型参数朝着更优的方向前进。
在具体算法中，一阶矩估计通常使用指数加权移动平均（exponential weighted moving average），简称为 "Momentum"。它记录了过去梯度的移动平均值，使得更新具有一定的惯性，有助于克服一些局部极小值，从而更容易到达全局最优值。
二阶矩估计：继续在山谷的比喻中，二阶矩估计是告诉你山谷的曲率信息。在优化算法中，二阶矩估计告诉我们当前位置斜率（梯度）的变化率。它是梯度的平方的平均值，反映了损失函数曲面的形状，从而帮助我们更准确地选择学习率。
在具体算法中，二阶矩估计通常使用指数加权移动平均的平方来计算，它记录了过去梯度平方的移动平均值。

在优化算法中，将一阶矩估计和二阶矩估计结合起来，通常可以得到更好的优化效果。Adam 算法就是一个结合了这两种估计的自适应优化算法，它根据一阶矩估计（梯度的移动平均值）和二阶矩估计（梯度平方的移动平均值）来自适应地调整学习率，以便更有效地更新模型参数，从而加快收敛速度并提高优化的稳定性。

先说核心结论：SGDM训练慢，但收敛性更好，训练也更稳定，训练和验证间的gap也较小。而Adam则正好相反。

有人研究过几大优化器在一些经典任务上的表现。如下是在图像分类任务上，不同优化器的迭代次数和ACC间关系。

SGD > Adam Which One Is The Best Optimizer: Dogs-VS-Cats Toy Experiment

训练集上

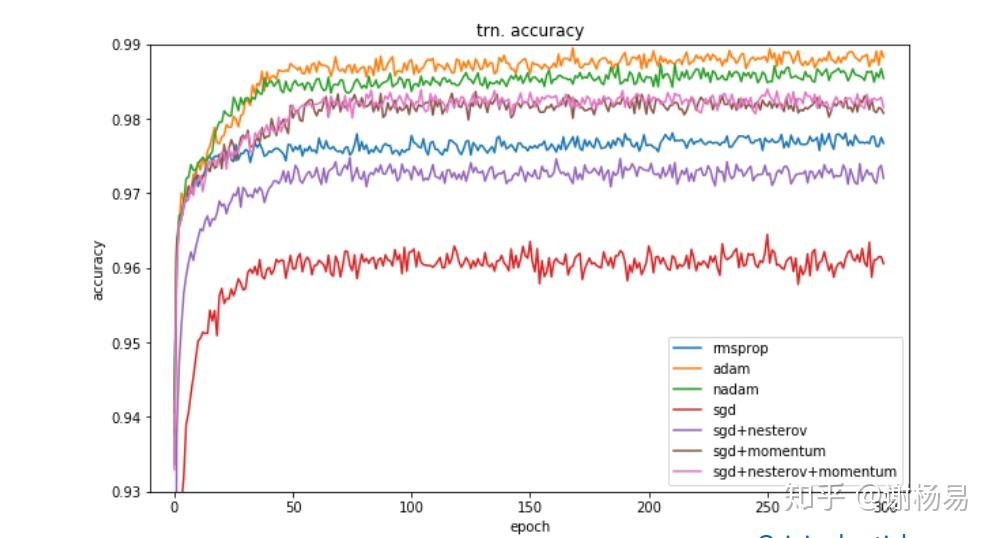
验证集上

可见

优化器对ACC影响也挺大的，比如上图Adam比SGD高了接近3个点。故选择一个合适的优化器也很重要。
Adam收敛速度很快，SGDM相对要慢一些，但最终都能收敛到比较好的点
训练集上Adam表现最好，但验证集上SGDM最好。可见SGDM在训练集和验证集一致性上，比Adam好。

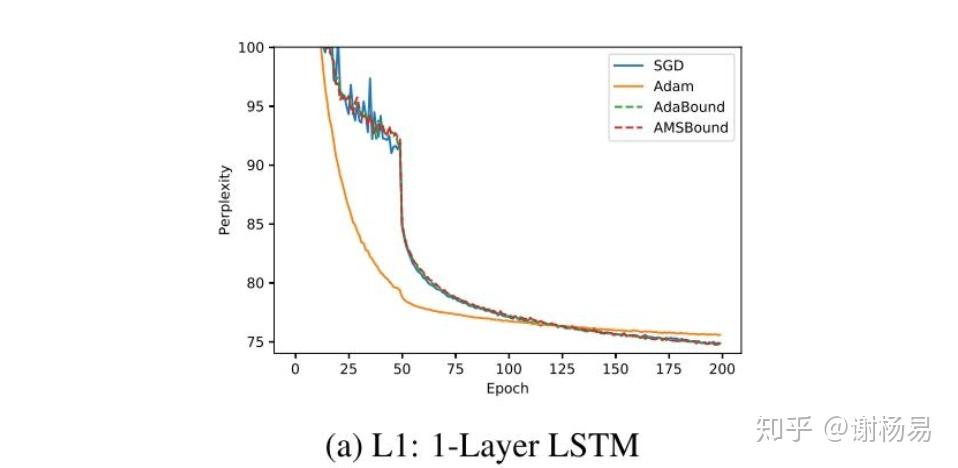
LSTM模型上，可见Adam比SGDM收敛快很多。最终结果SGDM稍好，但也差不多。

如下图所示，SGDM在CV里面应用较多，而Adam则基本横扫NLP、RL、GAN、语音合成等领域。所以我们基本按照所属领域来使用就好了。比如NLP领域，Transformer、BERT这些经典模型均使用的Adam，及其变种AdamW。

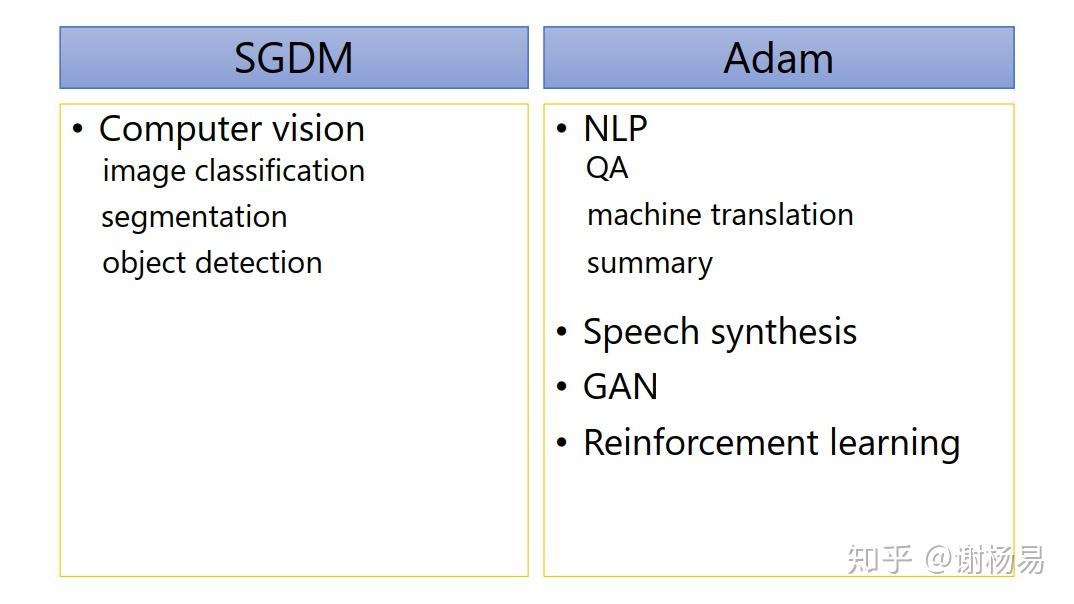
更详细的内容，欢迎阅读我的文章

谢杨易：机器学习2 -- 优化器（SGD、SGDM、Adagrad、RMSProp、Adam）

作者简介：

腾讯算法研究员。硕士毕业于中国科学院大学。在阿里和腾讯工作多年，拥有丰富的搜索和推荐算法经验。CSDN博客专家，原创文章100多篇。发表专利15个，其中已授权6个。

谢杨易--腾讯T11应用算法研究员，擅长搜索推荐算法谢杨易：精通推荐算法1：为什么需要推荐系统（系列文章，建议关注）谢杨易：精通推荐算法2：推荐系统分类和技术架构（面试必备）谢杨易：推荐算法架构1：召回（系列连载，建议关注）谢杨易：推荐算法架构2：粗排（体系化总结）谢杨易：推荐算法架构3：精排（万字长文）谢杨易：推荐算法架构4：重排（面试必备）

这是观看阿B的视频深度学习中的数学的ep15,16,17，推荐配合视频食用：

https://www.bilibili.com/video/BV1e94y1N7u5

我们这里默认了读者是有基本的数学和深度学习基础，主要记录一些重要的知识点。

我们这里依次复习几个优化器（参考 Deep Learning 之最优化方法）+ weight decay：

首先是最简单的SGD，这里不再赘述（注意这里的 $\\epsilon$ 是学习率）：

$g\\leftarrow\\frac1m\ abla_{\\boldsymbol{\ heta}}\\sum_iL(f(x^{(i)};\\boldsymbol{\ heta}),\\boldsymbol{y}^{(i)}) \\\\ \\begin{array}{l}\\Delta\ heta\\leftarrow- \\epsilon \\odot g\\\\\ heta\\leftarrow\ heta+\\Delta\ heta\\end{array}\\\\\\$ 那SGD有什么问题呢？子曰，要因材施教，那我们的公式 $\ heta\\leftarrow\ heta- \\epsilon \\odot g$ 可以看出，不同的层的梯度 $g$ 用的学习率 $\\epsilon$ 是一样的，那不同的层的梯度可能数量级不同，如果 $\\epsilon$ 数量级相比梯度太大（学习率过大），肯定梯度飞掉了；而相比梯度太小（学习率过小），会导致参数几乎没怎么更新。

所以，我们希望优化器能因材施教，即因“梯度”施“学习率”（自适应学习率）。具体的指导纲领自然是如果梯度大，就把学习率变小（陡峭的地区学习率自然应该小）；如果梯度小，就把学习率变大（平坦的地区学习率自然应该大）。但是学习率很小一定是好事嘛？那很有可能太小会掉到局部最小值，那我们最好加入一个动量，其实就是对学习率加一个指数移动平均（EMA）： $\\epsilon_t=\\alpha \\hat{ \\epsilon}_t +(1-\\alpha)\\epsilon_{t-1}\\\\$

具体来说怎么做呢？我们依次介绍一步步改进：

对前一个纲领，我们考虑历史梯度平方和（平方其实就是二阶矩），用 $r$ 表示： $r=\\sum _{i=1}^tg_i^2$ 。那梯度大其实就是 $r$ 大，梯度小就是 $r$ 小，很显然让学习率和 $\\frac{1}{\\sqrt{r}}$ 成正比即可（为了和 $g$ 数量级相同）。很显然，在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小）。但是我们这里 $r$ 是单调递增的，万一出现一个巨大的异常值 $g_t$ ， $r$ 会一直大下去，那缺点自然是使得学习率过早，过量的减少。

对后一个纲领，我们很容易就想到：既然刚刚是 $r$ 上出问题（单调递增），那我们对 $r$ 作一个EMA不就行了，那很自然就提出了RMSProp。

很快人们意识到，EMA这么香，为什么只对梯度二阶矩（平方）和做EMA，为什么不能在参数更新的时候对本来的 $g$ 也做一次EMA？这就出现了我们大名鼎鼎的Adam算法。

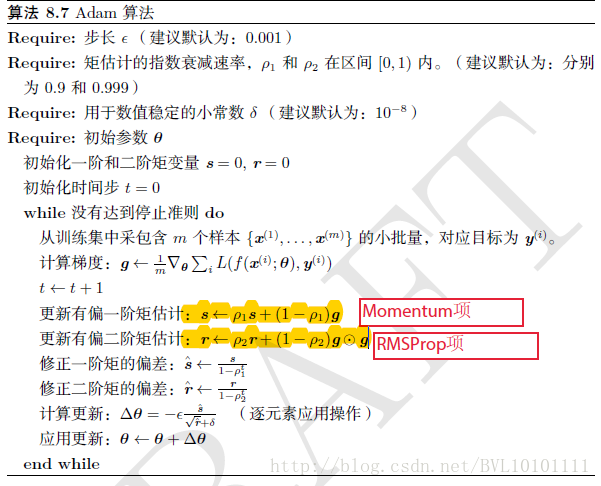
注意其中的“修正偏差”是因为一开始的 $s_0,r_0$ 为0，那一开始的 $s_i$ 偏小，那我们让其稍微大一些；当 $t$ 很大，我们显然可以看到分母均几乎为1，不再影响。

那Adam似乎已经很完美了，但是终于有人注意到一个魔鬼细节，藏在weight decay中（W就是从这里来的，n class="nolink">Adam with decoupled Weight decay）！weight decay是一种常用的正则化手段，其实就是减去梯度的时候再减去固定比例自己的参数值，本来的正则化项是： $w_{t+1}=w_t-\\alpha_t\\cdot\ abla(f(w_t)+\\frac{\\lambda^{}}2||w_t||_2^2) \\\\$ 求完梯度就是： $w_{t+1}=w_t-\\alpha_t\\cdot (\ abla f(w_t) + \\lambda w_t )\\\\$

Adam在使用weight decay是在所有计算完成之前，在计算梯度的时候就加入weight decay，那在计算梯度的时候会加上对正则项求梯度的结果，那么如果本身比较大的一些权重对应的梯度也会比较大，由于Adam计算步骤中减去项会有除以梯度平方的累积，使得减去项偏小（Adam会误以为大权重是大梯度）。按weight decay，越大的权重应该惩罚越大，但是在Adam并不是这样。

解决方法再简单不过：在最后加入weight decay呗！我们这里给出了Adam和AdamW的算法对比（只差了一行）：